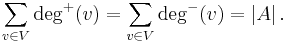Directed graph
A directed graph or digraph is a pair 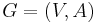 (sometimes
(sometimes 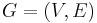 ) of:[1]
) of:[1]
- a set V, whose elements are called vertices or nodes,
- a set A of ordered pairs of vertices, called arcs, directed edges, or arrows (and sometimes simply edges with the corresponding set named E instead of A).
It differs from an ordinary or undirected graph, in that the latter is defined in terms of unordered pairs of vertices, which are usually called edges.
Sometimes a digraph is called a simple digraph to distinguish it from a directed multigraph, in which the arcs constitute a multiset, rather than a set, of ordered pairs of vertices. Also, in a simple digraph loops are disallowed. (A loop is an arc that pairs a vertex to itself.) On the other hand, some texts allow loops, multiple arcs, or both in a digraph.
Contents |
Basic terminology
An arc 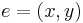 is considered to be directed from
is considered to be directed from  to
to  ;
;  is called the head and
is called the head and  is called the tail of the arc;
is called the tail of the arc;  is said to be a direct successor of
is said to be a direct successor of  , and
, and  is said to be a direct predecessor of
is said to be a direct predecessor of  . If a path made up of one or more successive arcs leads from
. If a path made up of one or more successive arcs leads from  to
to  , then
, then  is said to be a successor of
is said to be a successor of  , and
, and  is said to be a predecessor of
is said to be a predecessor of  . The arc
. The arc 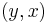 is called the arc
is called the arc 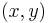 inverted.
inverted.
A directed graph G is called symmetric if, for every arc that belongs to G, the corresponding inverted arc also belongs to G. A symmetric loopless directed graph is equivalent to an undirected graph with the pairs of inverted arcs replaced with edges; thus the number of edges is equal to the number of arcs halved.
An orientation of a simple undirected graph is obtained by assigning a direction to each edge. Any directed graph constructed this way is called an oriented graph. A distinction between a simple directed graph and an oriented graph is that if  and
and  are vertices, a simple directed graph allows both
are vertices, a simple directed graph allows both 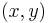 and
and 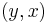 as edges, while only one is permitted in an oriented graph.[2][3][4]
as edges, while only one is permitted in an oriented graph.[2][3][4]
A weighted digraph is a digraph with weights assigned for its arcs, similarly to the weighted graph. A digraph with weighted edges in the context of graph theory is called a network.
The adjacency matrix of a digraph (with loops and multiple arcs) is the integer-valued matrix with rows and columns corresponding to the digraph nodes, where a nondiagonal entry 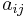 is the number of arcs from node i to node j, and the diagonal entry
is the number of arcs from node i to node j, and the diagonal entry 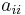 is the number of loops at node i. The adjacency matrix for a digraph is unique up to the permutations of rows and columns.
is the number of loops at node i. The adjacency matrix for a digraph is unique up to the permutations of rows and columns.
Another matrix representation for a digraph is its incidence matrix.
See Glossary of graph theory#Direction for more definitions.
Indegree and outdegree
For a node, the number of head endpoints adjacent to a node is called the indegree of the node and the number of tail endpoints is its outdegree.
The indegree is denoted 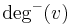 and the outdegree as
and the outdegree as 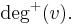 A vertex with
A vertex with 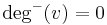 is called a source, as it is the origin of each of its incident edges. Similarly, a vertex with
is called a source, as it is the origin of each of its incident edges. Similarly, a vertex with 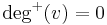 is called a sink.
is called a sink.
The degree sum formula states that, for a directed graph,
If for every node v ∈ V, 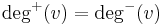 , the graph is called a balanced digraph.[5]
, the graph is called a balanced digraph.[5]
Digraph connectivity
A digraph G is called weakly connected (or just connected[6]) if the undirected underlying graph obtained by replacing all directed edges of G with undirected edges is a connected graph. A digraph is strongly connected or strong if it contains a directed path from u to v and a directed path from v to u for every pair of vertices u,v. The strong components are the maximal strongly connected subgraphs.
Classes of digraphs
A directed acyclic graph or acyclic digraph is a directed graph with no directed cycles. Special cases of directed acyclic graphs include the multitrees (graphs in which no two directed paths from a single starting node meet back at the same ending node), oriented trees or polytrees (the digraphs formed by orienting the edges of undirected acyclic graphs), and the rooted trees (oriented trees in which all edges of the underlying undirected tree are directed away from the root).
A tournament is an oriented graph obtained by choosing a direction for each edge in an undirected complete graph.
In the theory of Lie groups, a quiver Q is a directed graph serving as the domain of, and thus characterizing the shape of, a representation V defined as a functor, specifically an object of the functor category FinVctKF(Q) where F(Q) is the free category on Q consisting of paths in Q and FinVctK is the category of finite dimensional vector spaces over a field K. Representations of a quiver label its vertices with vector spaces and its edges (and hence paths) compatibly with linear transformations between them, and transform via natural transformations.
See also
Notes
- ^ Bang-Jensen & Gutin (2000). Diestel (2005), Section 1.10. Bondy & Murty (1976), Section 10.
- ^ Diestel (2005), Section 1.10.
- ^ Weisstein, Eric W., "Oriented Graph" from MathWorld.
- ^ Weisstein, Eric W., "Graph Orientation" from MathWorld.
- ^ Satyanarayana, Bhavanari; Prasad, Kuncham Syam, Discrete Mathematics and Graph Theory, PHI Learning Pvt. Ltd., p. 460, ISBN 9788120338425; Brualdi, Richard A. (2006), Combinatorial matrix classes, Encyclopedia of mathematics and its applications, 108, Cambridge University Press, p. 51, ISBN 9780521865654.
- ^ Bang-Jensen & Gutin (2000) p. 19 in the 2007 edition; p. 20 in the 2nd edition (2009).
References
- Bang-Jensen, Jørgen; Gutin, Gregory (2000), Digraphs: Theory, Algorithms and Applications, Springer, ISBN 1-85233-268-9, http://www.cs.rhul.ac.uk/books/dbook/
(the corrected 1st edition of 2007 is now freely available on the authors' site; the 2nd edition appeared in 2009 ISBN 1848009976). - Bondy, John Adrian; Murty, U. S. R. (1976), Graph Theory with Applications, North-Holland, ISBN 0-444-19451-7, http://www.ecp6.jussieu.fr/pageperso/bondy/books/gtwa/gtwa.html.
- Diestel, Reinhard (2005), Graph Theory (3rd ed.), Springer, ISBN 3-540-26182-6, http://www.math.uni-hamburg.de/home/diestel/books/graph.theory/ (the electronic 3rd edition is freely available on author's site).
- Harary, Frank; Norman, Robert Z.; Cartwright, Dorwin (1965), Structural Models: An Introduction to the Theory of Directed Graphs, New York: Wiley.
- Number of directed graphs (or digraphs) with n nodes., http://oeis.org/A000273